euler_vanderpol.py

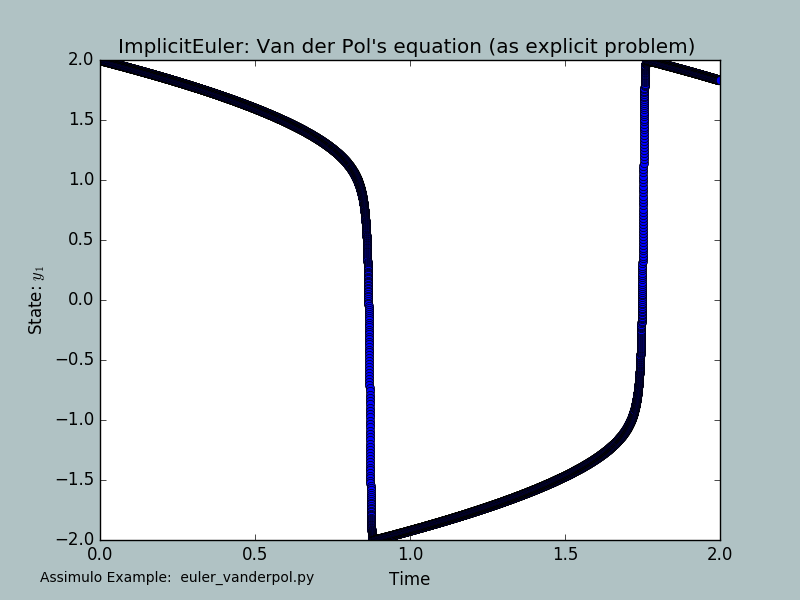
assimulo.examples.euler_vanderpol.run_example(with_plots=True)

Example for the use of the implicit Euler method to solve Van der Pol’s equation

\[\begin{split}\dot y_1 &= y_2 \\ \dot y_2 &= \mu ((1.-y_1^2) y_2-y_1)\end{split}\]

with \(\mu=\frac{1}{5} 10^3\).

on return:

• exp_mod problem instance
• exp_sim solver instance

---

Final Run Statistics: ImplicitEuler: Van der Pol's equation (as explicit problem)  

 Number of steps                 : 20001
 Number of function evaluations  : 45617
 Number of Jacobian evaluations  : 953
 Number of nonlinear iterations  : 25616

Solver options:

 Solver            : ImplicitEuler
 Solver type       : fixed step size
 Step size         : 0.0001

Simulation interval    : 0.0 - 2.0 seconds.
Elapsed simulation time: 2.68663907051 seconds.

Note

Press [source] (to the top right) to view the example.