cvode_with_initial_sensitivity.py

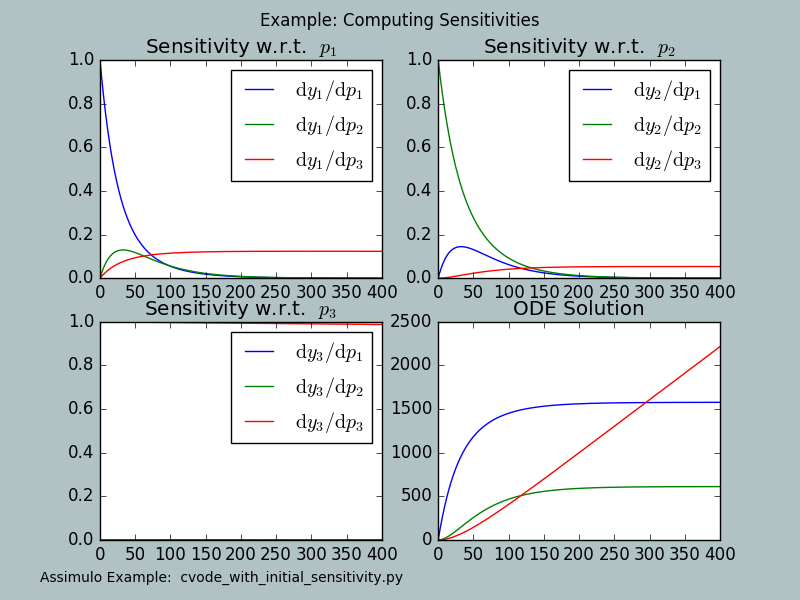
assimulo.examples.cvode_with_initial_sensitivity.run_example(with_plots=True)

This example shows how to use Assimulo and CVode for simulating sensitivities for initial conditions.

$$\begin{split}\dot y_1 &= -(k_{01}+k_{21}+k_{31}) y_1 + k_{12} y_2 + k_{13} y_3 + b_1\\ \dot y_2 &= k_{21} y_1 - (k_{02}+k_{12}) y_2 \\ \dot y_3 &= k_{31} y_1 - k_{13} y_3\end{split}$$

with the parameter dependent inital conditions $y_1(0) = 0, y_2(0) = 0, y_3(0) = 0$ . The initial values are taken as parameters $p_1,p_2,p_3$ for the computation of the sensitivity matrix, see http://sundials.2283335.n4.nabble.com/Forward-sensitivities-for-initial-conditions-td3239724.html

on return:

• exp_mod problem instance
• exp_sim solver instance

---

Final Run Statistics: Example: Computing Sensitivities 

 Number of steps                                       : 139
 Number of function evaluations                        : 164
 Number of Jacobian evaluations                        : 3
 Number of function eval. due to Jacobian eval.        : 9
 Number of error test failures                         : 2
 Number of nonlinear iterations                        : 160
 Number of nonlinear convergence failures              : 0
 Number of sensitivity evaluations                     : 164
 Number of function eval. due to sensitivity eval.     : 984
 Number of sensitivity nonlinear iterations            : 0
 Number of sensitivity nonlinear convergence failures  : 0
 Number of sensitivity error test failures             : 0

Sensitivity options:

 Method                   : SIMULTANEOUS
 Difference quotient type : CENTERED
 Suppress Sens            : False

Solver options:

 Solver                   : CVode
 Linear multistep method  : BDF
 Nonlinear solver         : Newton
 Linear solver type       : DENSE
 Maximal order            : 5
 Tolerances (absolute)    : 1e-06
 Tolerances (relative)    : 1e-07

Simulation interval    : 0.0 - 400.0 seconds.
Elapsed simulation time: 0.0260779857635 seconds.

Note

Press [source] (to the top right) to view the example.